1. Un estudios sobre los gustos musicales de los estudiantes en una universidad, se encuestó un total de 70 estudiantes, quienes manifestaron sus gustos de la siguiente manera:
20 la música Salsa 23 el Rock 40 las Baladas 10 Baladas y Salsa 13 Baladas y Rock
13 Baladas y Rock 5 Rock y Salsa 3 Salsa, Rock y las Baladas
Mediante un diagrama de Venn determine el número de estudiantes que les gusta:
a. Solamente baladas
b. La Salsa y el Rock pero no las baladas
c. El Rock y las Baladas pero no la Salsa
2. Un producto se arma en tres etapas. En la primera etapa hay 5 lineas de armado, en la segunda 4 lineas de armado y en la tercera 6 lineas de armado. ¿ De cuantas formas puede moverse el producto en el proceso de armado ?
R/
Principio de la Multiplicación
5*4*6 = 120
3. En Colombia las placas de los carros están formados por tres números y tres letras.
a. ¿ Cuántas placas se pueden generar en estas condiciones?
R/
Se puede escoger de 10 maneras diferentes así que:
3 números 10*10*10 = 1000
3 letras 26 maneras diferentes
26*26*26 = 17576
17576*1000 = 17576000
b. En el caso que para una ciudad como Medellín se asignen solamente las placas cuya primera letra es M o N. ¿ Cuantos automóviles pueden estar matriculados en Medellin?
R/
Las letras serian 24 entonces se dice que:
24*24*24 = 13824 + 1000 = 13824000
4. Un vendedor de automóviles nuevos quiere impresionar a sus clientes potenciales con la cantidad posible de diferentes combinaciones de que se dispone. Un modelo presenta tres tipos de motores, dos transmisiones, cinco colores de carrocería y dos colores de interiores. ¿ Cuantas posibilidades de elección existen respecto a estas opciones?
R/
Principio de la Multiplicación
3*2*5*2 = 60 posibilidades de elección
5. Explique la diferencia entre Permutaciones y Combinaciones
R/
6. Se juegan 5 dados ¿ De cuantas maneras pueden caer?
R/
5 Dados x 6 Caras = 30 caras
n= 30 caras
r = 5 dados
nCr= n!/(n-r)!r!
30C5 = 30!/(30-5)!5! = 30!/25!5! = 30*29*28*27*26*25!/25!5! = 17100720/120
= 142506 Formas de Caer
7. En un concurso de belleza se suele escoger primero 15 semifinalistas y luego se eligen 5 finalistas ¿De cuántas maneras se pueden ocupar las cinco primeras posiciones entre las 15 semifinalistas?
R/
n = 15 Semifinalistas
r = 5 Finalistas
15C5 = 15!/(15-5)!5! = 15!/10!5! = 15*14*13*12*11*10!/10!5! = 360360/120
= 3003 Maneras de ocupar las 5 primeras posiciones
8. Una liga de fútbol esta integrada por 6 equipos. ¿Cuantos resultados diferentes posibles habrá en la temporada? (Supón que ningún equipo termina la temporada empatado con otro).
R/
6! = 720
6*5*4*3*2*1 = 720 Resultados diferentes en la temporada
10. La junta directiva de la compañia ABC esta compuesta por 15 miembros ¿De cuántas formas se puede elegir presidente, vicepresidente y secretario?
R/
n = 15 miembros
r = 3
15P3 = 15!/(15-3)! = 15!/12! = 15*14*13*12!/12! = 2730 Formas de elegir
11. Se va a elegir un comité de 5 miembros entre un grupo de 7 candidatos. ¿De cuantas formas se puede hacer esto? ¿De cuantas maneras si los 7 candidatos van a ocupar cargos distintos? ¿De cuantas maneras se pueden ocupar los cargos?
R/
n = 7 candidatos
r = 5 miembros
7C5 = 7!/(7-5)!5! = 7!/2! = 7*6*5*4*3*2!/2! = 420 Maneras de ocupar los cargos















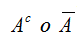



 la cual se puede interpretar como probabilidad de A dado B.
la cual se puede interpretar como probabilidad de A dado B.