SEMANA 3 OPERACIONES CON SUCESOS

En el contexto probabilístico, denominamos suceso a cualquier subconjunto de un espacio muestral; esto es, a cualquier posible resultado de un experimento aleatorio. 

Suceso elemental

Un suceso se dice que es un suceso elemental si está formado por un único elemento del espacio muestral. Por ejemplo, al tirar un dado el suceso consistente en obtener un cinco.

Suceso Compuesto

Un suceso se dice que es un suceso compuesto si está formado por más de un elemento del espacio muestral. En el mismo ejemplo anterior obtener un número par, es decir, que salga un 2 o un 4 o un 6. 

Entre los diferentes sucesos destacaremos los siguientes:

Suceso seguro

El suceso seguro es aquél que está formado por todos los resultados posibles del espacio muestral (E), es decir aquél que se cumple siempre. Por ejemplo al tirar un dado cúbico obtener un número del uno al seis.

Suceso imposible

El suceso imposible es aquél que no ocurre nunca. Se expresa con el símbolo Ø. Por ejemplo, obtener un ocho al tirar un dado cúbico.

   

Suceso contrario o complementario de otro suceso

Se define el suceso contrario a A como el suceso que acontece cuando no ocurre A. EL suceso contrario a obtener un número par es obtener uno impar. Suele denotarse como: 

 

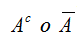
Unión de Sucesos:

Sean dos sucesos aleatorios A y B dentro de un espacio muestral. Se define la Unión de dos Sucesos A y B (o la Suma de dos Sucesos) como: 

A ∪ B = suceso formado por todos los elementos de A y todos los elementos de B

Propiedades de la Unión de Sucesos:

La unión de sucesos tiene las siguientes propiedades:

• Propiedad Conmutativa:  A ∪ B = B ∪ A
• Propiedad Asociativa: A ∪ (B ∪ C) = (A ∪ B) ∪ C
• Propiedad Impotente: A ∪ A = A
• Propiedad de Simplificación: A ∪ (A ∩ B) = A
• Propiedad Distributiva: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
• Elemento Neutro: A ∪ Ø = A
• Absorción: A ∪ E = E, donde E es el espacio muestral al que pertenece el suceso A

Ejemplos:

Experimento aleatorio de tirar un dado de 6 caras. Sean los sucesos A y B siguientes:

• Suceso A = que salga un número par = {2, 4, 6}
• Suceso B = que salga un múltiplo de 3 = {3, 6}

A ∪ B = {2, 4, 6} ∪ {3, 6} = {2, 3, 4, 6}

El experimento aleatorio de tirar un dado de 6 caras. Sean los sucesos A y B siguientes:

• Suceso A = que salga un número par = {2, 4, 6}
• Suceso B = que salga un número mayor de 4 = {5, 6}

A ∪ B = {2, 4, 6} ∪ {5, 6} = {2, 4, 5, 6}

PROBABILIDAD CONDICIONAL

El concepto  de probabilidad condicional surge cuando se quiere obtener la probabilidad de un evento A, y se tiene conocimiento que ya ocurrió otro evento B, relacionado al primero se denota con la cual se puede interpretar como probabilidad de A dado B.

Ejemplo: el evento B es tener la gripe, y el evento A es tener dolor de cabeza,  sería la probabilidad de tener dolor de cabeza cuando se está enfermo de gripe.